

|
|||||||||||||||||||
|
| SkyServer.org - HTM | ||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||
Definition
The starting point for the scheme to subdivide the sphere are the 8 spherical triangles with equal size -- the octahedron on the sphere (see figure 2 and first image of figure 1). A ``spherical triangle'' is given by three points on the unit sphere connected by great circle segments. The octahedron has six vertices, given by the intersection points of the x,y,z axes with the unit sphere, which we enumerate vo through v5 :
( 0, 0, 1 ) v
0
( 1, 0, 0 ) v
1
( 0, 1, 0 ) v
2
(1)
(-1, 0, 0 ) v
3
( 0, -1, 0 ) v
4
( 0, 0, -1 ) v
5
The first 8 nodes of the Spatial Index are defined as
v v v : S0 v v v : N0
1 5 2 1 0 4
v v v : S1 v v v : N1
2 5 3 4 0 3
(2)
v v v : S2 v v v : N2
3 5 4 3 0 2
v v v : S3 v v v : N3
4 5 1 2 0 1
The triangles are all given with the vertices traversed counterclockwise.
The construction of the next level makes use of this ordering.

|
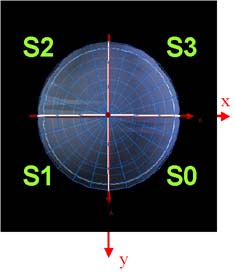 |
Figure 2: The 8 root nodes of the HTM quad-tree. The x,y,z axes form a right-handed system, i.e. the z axis points out of the paper on the left side and down through the paper on the right.
Iteration Step
A given spherical triangle (v0,v1,v2) with the vertices ordered counterclockwise is subdivided into four spherical triangles using the side-midpoints (w0,w1,w2) of the starting triangle
v + v
1 2
w = ------------
0 | v + v |
1 2
v + v
0 2
w = ------------
1 | v + v |
0 2
(3)
v + v
0 1
w = ------------
2 | v + v |
0 1
The four new triangles are given by
Triangle 0 : v w w
0 2 1
Triangle 1 : v w w
1 0 2
(4)
Triangle 2 : v w w
2 1 0
Triangle 3 : w w w
0 1 2
The node name of the new triangles is the name of the original
triangle with the triangle number appended. If the original node name
was S0, the new node names are S00, S01,
S02 and S03 (see figure 3). This
iteration can be repeated to any desired depth. The number of leaf
nodes N at a given level depth d is given by
d
N(d) = 8 * 4
(5)
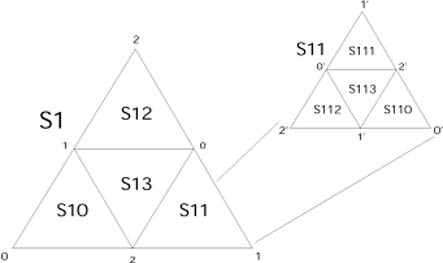
Figure 3:The quad tree is obtained by subdividing spherical triangles
into four smaller ones. The procedure is repetitive, and the naming
scheme is just to add the number of the triangle to the parent's name.
The recursive process defined by equations (3,4) defines what we call the Hierarchical Triangular Mesh (HTM). The HTM is very well suited to build a Spatial Index of 3-dimensional data that has an inherent spherical distribution - like in Astronomy and Earth Sciences.
Properties and Statistics
In addition to the number of nodes per iteration level calculated in (5) we can give the triangle size/area for each level. The triangles will not have the same size or area but the variation is within tolerable limits. (See figure 4)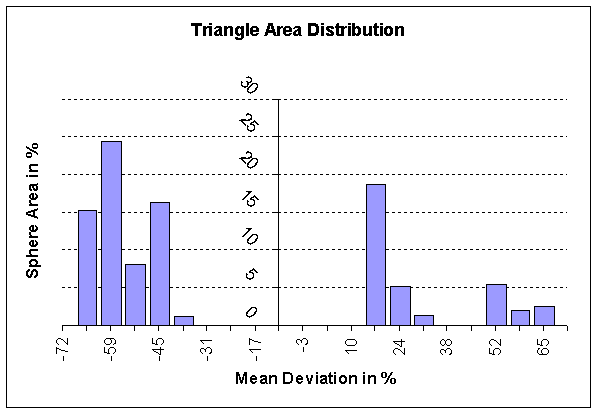
Figure 4: The triangle area distribution shown here is valid for any
level in the quad-tree (except for the first 3-4 levels where there is
much less scatter). The triangle areas are distributed about 70%
around the mean area. The exact mean area is of course always 1/4th of the
previous level; starting from the octahedron (level 0) where the area of
one triangle is Pi/2. The figure shows that about half the triangles are
less than average size and the other half is bigger than average size
(for each level).
The shapes of the triangles are also different. For each level there are more and more differently-shaped triangles. The shape difference is kept within certain limits, though - the maximal inner angle of a triangle never exceeds Pi/2 and is never less than Pi/4. The sidelengths are also within a fixed minimal and maximal value per level (see figure 5).
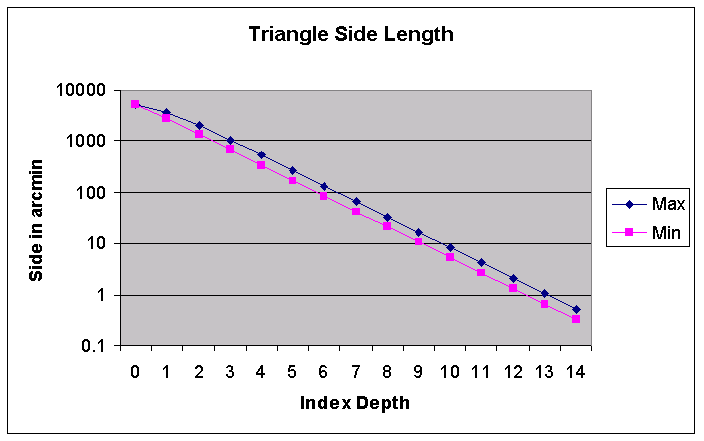
Figure 5: The length of the triangle sides is displayed per level.
The smallest sidelength encountered is always Pin+1
- this is the subdivision of the side that lies on the edge of the
original octahedron. All the other sides are longer. The maximal
sidelength is always at the center of the level-0 octahedron
triangle. It can be shown that the maximum never extends the minimum
by more than a factor of Pi/2
The folowing table gives an indication of pixel area and number of htm leaves in HTMs of given depths
| Level | Area(arcmin^2) | Num Leaves | |
|---|---|---|---|
| Low | High | ||
| 10 | 14 | 29 | 8,388,608 |
| 11 | 3 | 7.3 | 33,554,432 |
| 12 | 0.86 | 1.8 | 134,217,728 |
| 13 | 0.21 | 0.45 | 536,870,912 |
| 14 | 0.05 | 0.11 | 2,147,483,648 |
| 15 | 0.01 | 0.028 | 8,589,934,592 |
| 20 | 1.3E-05 | 2.8E-05 | 8,796,093,022,208 |
| 25 | 1.0E-08 | 2.1E-08 | 9,007,199,254,740,922 |
William O'Mullane
Last Modified :Tuesday, December 26, 2006 at 3:52:09 PM
, $Revision 1.5 $
 The Hierarchical Triangular Mesh
The Hierarchical Triangular Mesh